Onderwerpen:
- Vrijheidsgraden in de wielgeleiding
- Scharnieren in de wielgeleiding
- Geleiders in de wielgeleiding
- Vrijheidsgraden berekenen
Vrijheidsgraden in de wielgeleiding:
In de wielophanging van een auto zitten een aantal scharnieren (o.a. aan de draagarmen en schokdemper) die zorgen voor de vrijheidsgraden in de totale wielophanging. De wielgeleiding zorgt ervoor dat de mogelijke vrijheidsgraden van de mogelijke wielbewegingen tot slechts één of twee beperkt blijven. Als een wiel namelijk niet “vast” gehouden wordt, zal het vrij kunnen roteren, kantelen (in x en y richting), draaien, omhoog en omlaag bewegen. Het wiel is dan in principe “los” van de ophanging. Het kan elke richting op bewegen zonder “geleiding”. Elke net genoemde beweging is één vrijheidsgraad.
De wielophanging, dus de wielgeleiding, zorgt ervoor dat de bewegingsvrijheid wordt beperkt tot 1 vrijheidsgraad. Daarmee wordt bedoeld, dat het wiel in slechts 1 richting “vrij” kan bewegen, zonder invloed van de bestuurder. Die vrije beweging is de op-en-neer gaande beweging van het in- en uitveren. Het wiel kan onverhinderd in- en uitveren over een ongelijk wegdek.
De wielophanging van een auto wordt geconstrueerd met een aantal lijnscharnieren, kogelscharnieren en draai- schuifscharnieren. Deze scharnieren hebben allemaal invloed op elkaar. Een scharnier te veel zorgt voor te veel vrijheidsgraden (dus het wiel kan ongewild verschillende richtingen op bewegen) of voor 0 vrijheidsgraden (het wiel kan dan niet bewegen en dus ook niet in- en uitveren).
Scharnieren in de wielgeleiding:
Lijnscharnier:
Dit lijnscharnier kan in 1 richting bewegen; omhoog en omlaag. Dit zorgt voor 1 vrijheidsgraad.
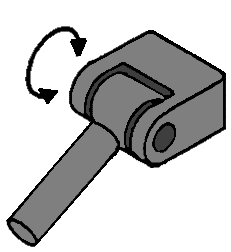
Kogelscharnier:
Met dit scharnier kunnen de betreffende delen ten opzichte van elkaar 3 bewegingen maken; een knik-, rol- en draaibeweging. Dit scharnier heeft 3 vrijheidsgraden, want als het scharnier “los” is, kan het 3 vrije bewegingen maken (zie pijlen).
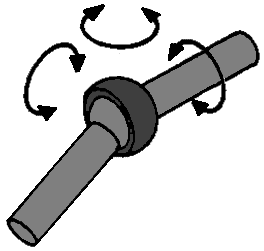
Draai- schuifscharnier:
Dit scharnier kan 2 bewegingen maken; een draaiende en een in- en uitschuivende beweging. In principe is dit een voorbeeld van een schokdemper (van een McPherson veerpoot). Deze 2 bewegingen zorgen ervoor dat het draai- schuifscharnier 2 vrijheidsgraden heeft.
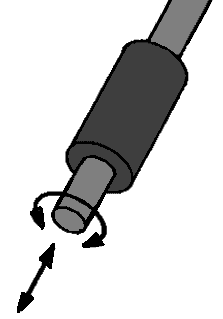
Geleiders in de wielgeleiding:
Om van diverse soorten scharnieren een wielophanging te maken, moeten scharnieren soms samengevoegd worden op 1 object, bijv. een draagarm. Deze draagarm noemen we dan een geleider. Hieronder zijn een paar voorbeelden te zien van deze geleiders:
Lijnscharnier met kogelgewricht:
Dit is een typisch voorbeeld van een draagarm, die aan de kant van het lijnscharnier verbonden zit met de carrosserie (of subframe) en aan de kant van het kogelscharnier verbonden is met het fusee. Als dit hele scharnier los is, kan het zowel de bewegen in de bewegingsrichting van het lijnscharnier (1 richting) als de 3 richtingen van het kogelscharnier. Het lijnscharnier heeft immers 1 vrijheidsgraad en het kogelscharnier heeft er 3. Omdat dit gedeelte als 1 geleider wordt gezien, kunnen de vrijheidsgraden bij elkaar opgeteld worden. De 1 en de 3 maken het dan 4 vrijheidsgraden.
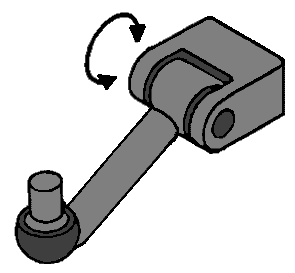
Dubbel kogelgewricht:
Een voorbeeld van een geleider met een dubbel kogelgewricht is de spoorstang met de binnenste en de buitenste spoorstangkogels. Elk kogelgewricht heeft 3 vrijheidsgraden, dus omdat het 1 geleider is, zouden deze bij elkaar opgeteld moeten worden. Echter, ze hebben de zelfde eigenrotatie, want als 1 kogelscharnier een roterende beweging maakt, dan maakt de ander dat ook. Dus 1 vrijheidsgraad van de eigenrotatie telt niet mee (zie de rode pijlen). De vrijheidsgraden zijn bij deze geleider in totaal 6, maar in de berekening die hierna volgt, vul je bij “eigenrotaties r” het getal 1 in. Deze 1 wordt er in de berekening dan weer vanaf getrokken.
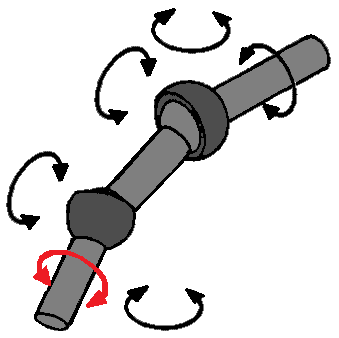
Draai- schuifscharnier met kogelgewricht:
Zoals eerder verteld, is een schokdemper een draai- schuifscharnier. Echter, bij elke McPherson veerpoot zit daar ook nog een kogelgewricht boven, ook al zou je dat in eerste instantie niet denken. Aan de bovenkant van de schokdemper zit nog een rubber. Dit rubber zorgt voor enige bewegingsvrijheid van de schokdemper en heeft daarmee ook de eigenschappen van een kogelgewricht. Een schokdemper heeft dus zowel de 2 vrijheidsgraden van het draai- schuifscharnier, als de 3 vrijheidsgraden van het kogelgewricht, wat samen 5 maakt. Ook nu is er sprake van een eigenrotatie, omdat de draaibeweging van het draai- schuifscharnier de zelfde beweging is als de draaibeweging van het kogelgewricht. Dus bij de “r” van eigenrotatie zal er 1 bij opgeteld moeten worden.
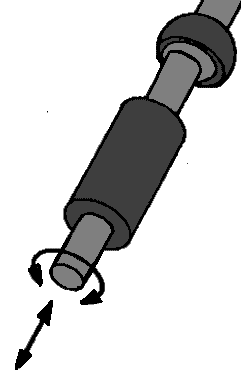
Vrijheidsgraden berekenen:
Aan de hand van de gegevens van de wielophanging kunnen het aantal vrijheidsgraden berekend worden. Om de formule hiervan goed in te vullen, moeten de scharnieren en geleiders in categorieën worden ingedeeld:
- L voor het aantal geleiders
- g voor het aantal gewrichten en scharnieren
- r voor het aantal eigenrotaties (zoals bij het dubbel kogelgewricht in 1 geleider)
Daarbij komen nog de letters:
- k voor het aantal wieldragers (in de meeste gevallen 1, omdat dit dan het fusee is)
- εfi voor het aantal vrijheidsgraden voor het totaal aantal gewrichten en scharnieren bij elkaar opgeteld.
F = 6 (k + L – g) -r + εfi
Voorbeeld:
In een wielophanging zitten: k 1 wieldrager (fusee), L 2 geleiders, g 5 gewrichten, r 2 eigenrotaties, εfi 15 totale vrijheidsgraden
In formulevorm is dit:
F = 6 (1 + 2 – 5) – 2 + 15
F = 6 x (-2) – 2 + 15
F = 1
Er is dus nu 1 vrijheidsgraad, dus dit is goed. Het wiel kan een zuivere op- en neergaande beweging maken.
Om dit te verduidelijken volgt hier een voorbeeld met een afbeelding van een wielophanging:
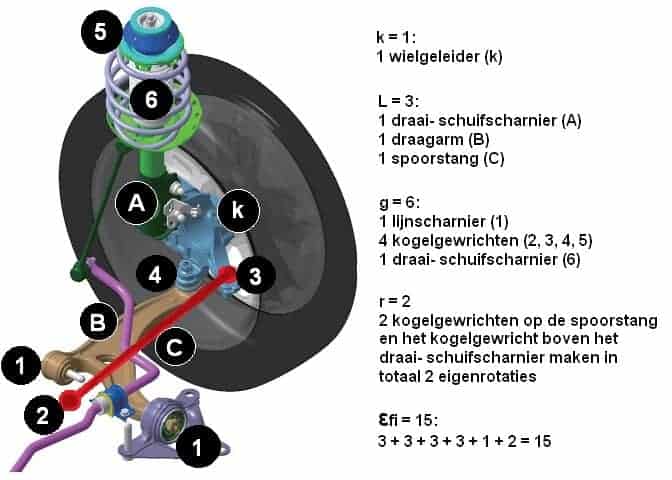
De onderstaande afbeelding is van een McPherson veerpoot met de bij behorende legenda. De letters A, B en C staan voor de geleiders en de cijfers 1 t/m 6 staan voor de scharnieren / gewrichten.
εfi zijn de vrijheidsgraden van de scharnieren bij elkaar opgeteld; dus 3 vrijheidsgraden per kogelgewricht (dus 4 x 3), 1 vrijheidsgraad van het lijnscharnier en 2 vrijheidsgraden van het draai- schuifscharnier.
De formule kan hiermee worden ingevuld:
F = 6 (k + L – g) -r + εfi
F = 6 (1 + 3 – 6) – 2 + 15
F = 6 x (-2) – 2 + 15
F = -12 – 2 + 15
F = -14 + 15
F = 1 vrijheidsgraad
