Onderwerpen:
- Uitspoor in de bocht
- Berekenen van de ingestuurde hoeken
Uitspoor in de bocht:
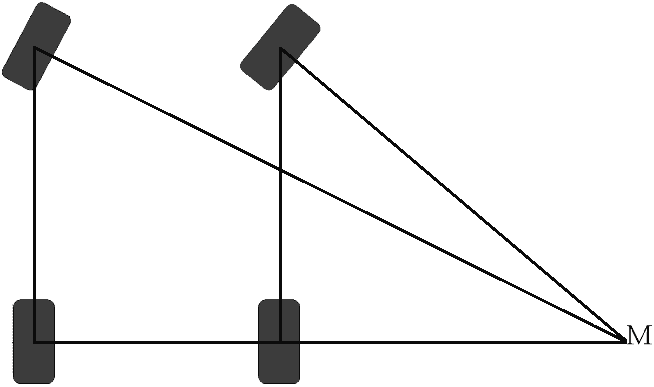
De voorwielen sturen in de bocht niet onder dezelfde hoek. Het binnenste wiel zal altijd een “scherpere” bocht maken dan het buitenste wiel. In de afbeelding is te zien waarom dat zo is.
In de afbeelding is te zien dat de lijnen vanaf de voorwielen uit komen in de hoek M. De hoek M is het gemeenschappelijk draaipunt van beide voorwielen. Wanneer de wielen onder de zelfde hoek zouden verdraaien, (de wielen staan dan beide in exact de zelfde positie), zouden de lijnen vanaf de wielen ook evenwijdig aan elkaar lopen tot in het oneindige. Ze vinden nooit het gemeenschappelijk draaipunt M. Daarom zullen de stuureigenschappen in deze situatie zeer slecht zijn. Dit hele principe wordt “uitspoor in de bocht” genoemd. Alle moderne auto’s zijn geconstrueerd met deze eigenschap.
Op gladde ondergronden, bijv. de vloer in de parkeergarage, is gepiep van de banden te horen bij het insturen. Dat komt door dit principe. Het binnenste wiel, dat een scherpere hoek maakt dan het buitenste, zal enige vorm van slip ondervinden. Dit wordt een stuurfout genoemd. Meer informatie over de stuurfout (en een grafiek) is te vinden op de pagina stuurfout.
Op deze pagina wordt uitgelegd hoe er met behulp van een aantal gegevens de ingestuurde hoeken (in graden) van beide voorwielen kunnen worden berekend.
Berekenen van de ingestuurde hoeken:
Voor het berekenen van de ingestuurde hoeken zijn de volgende gegevens nodig van het voertuig:
- Spoorbreedte
- Wielbasis
- Diameter draaicirkel
- Fusee afstand (op deze pagina houden we de fusee afstand gelijk aan de spoorbreedte)
- Bandenmaat (afhankelijk van berekening. Op deze pagina wordt er met de bandenmaat gerekend, maar er kan ook tot aan de bumperhoeken berekend worden. Echter, komen er dan nog meer hoeken bij).
| Spoorbreedte = 1600mm | Wielbasis = 3200mm |
| Diameter draaicirkel = 13,225m | Fuseeafstand = Spoorbreedte = 1600mm |
| Bandenmaat = 225 | L en L’ = onbekend |
Verklaring van de symbolen:
α = Alpha
β = Bèta
γ = Gamma
Deze letters zijn van het Griekse alfabet en worden vaak gebruikt voor berekeningen in hoeken.
L = de lengte
L’ = L met “accent” als toevoeging wat wiskundig veel wordt gebruikt. Er had net zo goed L2 kunnen staan. Zo had een 3e L twee accenten gekregen: L” .
Dat zelfde geld voor R”.
De hoeken Alpha, Bèta en Gamma liggen bij punt M.
Hoek Alpha + Gamma = hoek Bèta.
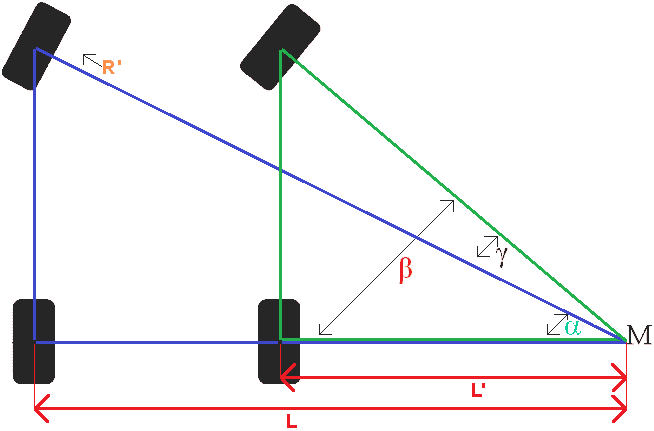
De gehele draaicirkel is 13,225 meter. R is de straal, dus dat is de halve draaicirkel (6612,5). In de afbeelding staat R’ gegeven. Deze R’ is geen vast gegeven. Deze moet berekend worden door de helft van de bandbreedte er vanaf te halen. Een andere manier is om de fusee afstand er vanaf te halen, maar op deze pagina houden we aan: Spoorbreedte = fusee afstand. Hieruit volgt de simpele berekening:
R = 6612,5 mm
R’ = R – halve bandbreedte
R’ = 6612,5 – (225 : 2)
R’ = 6612,5 – 112,5
R’ = 6500 mm
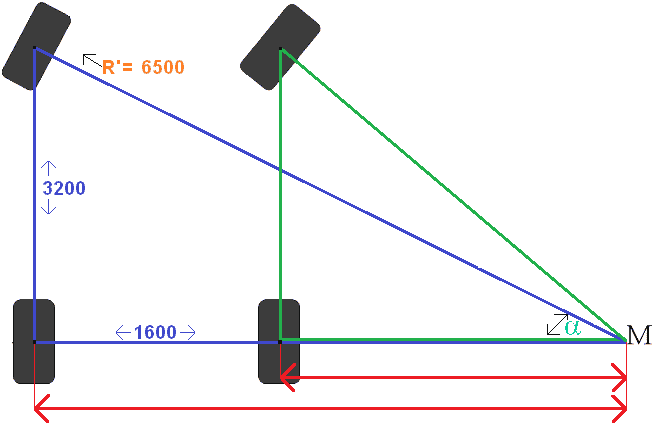
De R’ vullen we in de afbeelding in. Vervolgens berekenen we de hoek sin α (sinus Alpha) met de Sinusregel. Daarna berekenen we de overige hoeken met de Tangens en de Stelling van Pythagoras.
Hoekberekening met de Sinus:
Sin α = Overstaande zijde : Schuine zijde
Sin α = Wb : R’
Sin α = 3200 : 6500
Sin α = 0.492
Inv Sin α = 29,5°
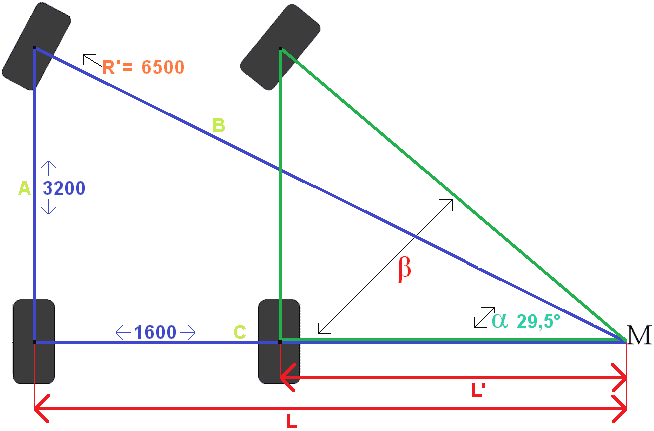
Uitleg over de berekening:
We willen Sin α berekenen. De sinus is overstaande zijde delen door de schuine zijde (geheugensteuntje: SIN = SOS).
Wb= wielbasis = 3200mm. R’ hebben we eerder berekend = 6500mm.
Vervolgens delen we dat door elkaar; dan hebben we Sin α = 0.492. Om dit getal vervolgens om te rekenen naar een hoek, toets je in de rekenmachine de knop sin-1 in (meestal eerst de Shift knop indrukken en dan op de Sin toets) gevolgd door de 0.492, of de knop ANS. Nu komt de hoek van 29,5 graden in beeld.
Sin α is nu bekend. Nu willen we eigenlijk tan β berekenen, maar dan hebben we de lengte L’ nodig. Deze moet als eerst berekend worden. Het antwoord van de berekening L’ gebruiken we dus om later Tan β te berekenen.
L’ = L – Spoorbreedte.
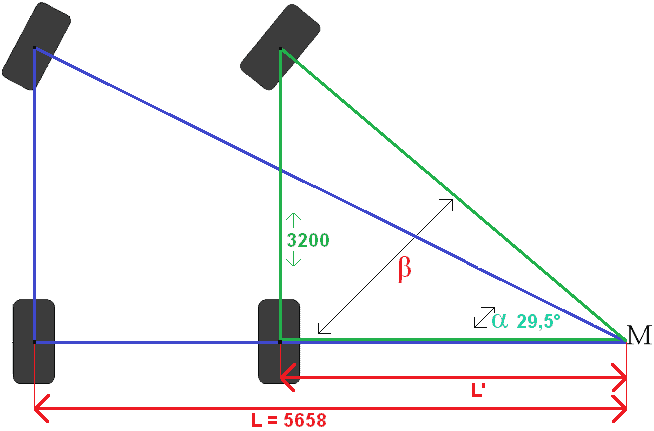
L berekenen we met de stelling van Pythagoras. De 2 zijden van de driehoek zijn bekend (6500 en 3200). De andere zijde van 1600 is de spoorbreedte die van band tot band loopt, dus die telt niet mee. We gaan de onderste zijde berekenen, die vanaf de linker achter band naar het gemeenschappelijk punt M loopt. De berekening gaat dus over de complete blauwe driehoek.
De stelling van Pythagoras ziet er als volgt uit:
A^2 + B^2 = C^2. (Het teken ^ is een symbool voor “macht”. Er staat dus A kwadraat + B kwadraat = C kwadraat. We formuleren het hier onder iets anders.
De lengte 3200 noemen we A, 6500 noemen we B en de onderste onbekende zijde noemen we C:
C^2 = 6500^2 – 3200^2
C^2 = 42250000 – 10240000
C^2 = 32010000^2
Om het kwadraat weg te werken, nemen we de wortel van het getal.
C^2 = √32010000
C = 5658mm.
Zijde C is in werkelijkheid lengte L.
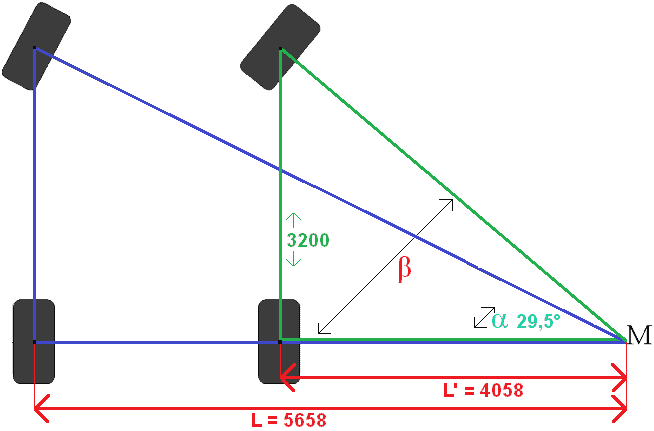
Nu kan L’ berekend worden. De volledige lengte L en de spoorbreedte zijn bekend, dus die twee kunnen eenvoudig van elkaar afgetrokken worden:
L’ = L – Spoorbreedte
L’ = 5658 – 1600
L’ = 4058mm
Nu zijn de Wb en L’ bekend. Twee van de drie zijden van de driehoek zijn bekend, dus dan kan met de Tangens de derde zijde worden berekend:
Hoekberekening met de Tangens:
Tan β = Overstaande zijde : Aanliggende zijde
Tan β = Wb : L’
Tan β = 3200 : 4058
Tan β = 0.789
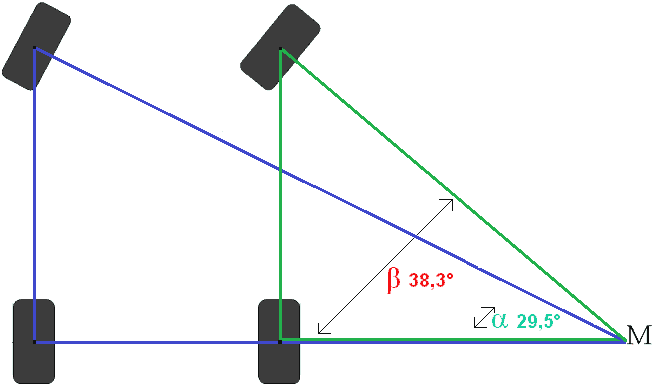
Inv Tan β = 38,3°
Uitleg over de berekening:
We willen Tan β berekenen. De tangens is overstaande zijde delen door de aanliggende zijde (geheugensteuntje: TAN = TOA).
Wb= wielbasis = 3200mm. L’ hebben we eerder berekend = 4058mm.
Vervolgens delen we dat door elkaar; dan hebben we Tan β = 0.789. Om dit getal vervolgens om te rekenen naar een hoek, toets je in de rekenmachine de knop tan-1 in (meestal eerst de Shift knop indrukken en dan op de Tan toets) gevolgd door de 0.789, of de knop ANS. Nu komt de hoek van 38,3 graden in beeld.
Nu zijn ingestuurde hoeken van beide voorwielen berekend. Het linker voorwiel staat onder een hoek van 29,5° en het rechter voorwiel onder een hoek van 38,3°. Dat betekent dat de ingestuurde hoek een verschil in beide wielen heeft van 8,8°. In een bocht naar links zal met de zelfde stuuruitslag de zelfde ingestuurde hoek ontstaan.
Op de pagina wielgeometrie worden meerdere wielstanden beschreven.
