Onderwerpen:
- Overbrengingsverhoudingen inleiding
- Kracht aan de wielen
- K-factor bepalen volgens de meetkundige reeks
- K-factor bepalen volgens de gecorrigeerde meetkundige reeks (de reeks van Jante)
- Overbrengingsverhoudingen bepalen (inleiding)
- Reductie van de 1e versnelling berekenen
- Reductie van de 5e versnelling berekenen (volgens de meetkundige reeks)
- Overige reducties berekenen (volgens de meetkundige reeks)
- Reducties berekenen volgens de gecorrigeerde meetkundige reeks (Reeks van Jante)
- Voertuigsnelheid per reductie berekenen (meetkundige reeks)
- Voertuigsnelheid per reductie berekenen (gecorrigeerde meetkundige reeks)
Overbrengingsverhoudingen inleiding:
De overbrengingsverhouding wordt bepaald door:
- Het aantal tanden van de tandwielen (zoals de versnellingsbak)
- De diameter van de poelies (zoals van de componenten die door de multiriem worden aangedreven)
In de afbeelding is te zien dat tandwiel A 20 tanden, en tandwiel B 40 tanden heeft. De verhouding is 40/20 = 2:1.
Dat betekent dat tandwiel A (aangedreven) twee omwentelingen maakt als tandwiel B één omwenteling maakt. Dit is in de praktijk eigenlijk nooit het geval. Er wordt altijd gezorgd voor een verhouding die nooit exact 2,00:1 is, omdat in het laatste geval bij iedere omwenteling de zelfde tanden in elkaar grijpen. Wanneer tandwiel B 39 tanden zou hebben (1,95:1) of 41 tanden (2,05:1) grijpen de tandwielen van A en B elke omwenteling een tandje verder in elkaar, waardoor de slijtage 20 keer minder is als bij de verhouding van 2:1.
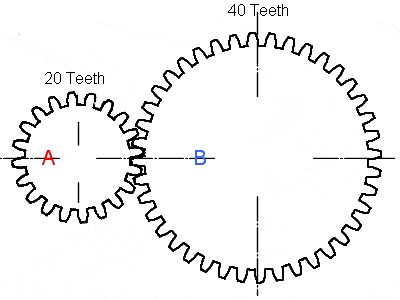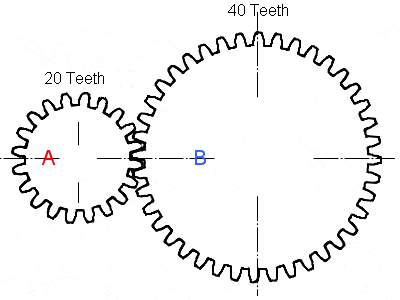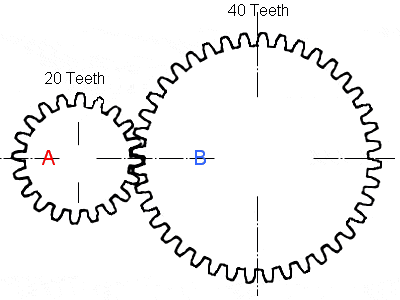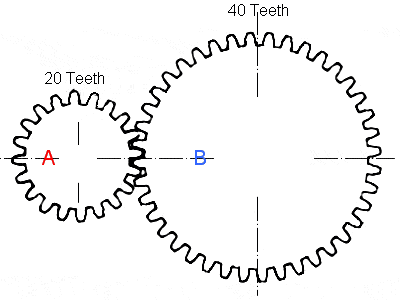
Een hoge overbrengingsverhouding (waarbij het drijvende tandwiel klein en het gedreven tandwiel groot is) geeft een hoge topsnelheid en een lage overbrengingsverhouding geeft meer trekkracht. In de versnellingsbak van een auto (in principe alle motorvoertuigen) wordt bij het ontwerp rekening gehouden met de doeleinden waarvoor de auto gebruikt gaat worden. Een auto die voornamelijk bedoeld is om een zware lading te vervoeren zal meer trekkracht bij lage versnellingen nodig hebben dan een sportauto die een hoge topsnelheid moet kunnen bereiken. De overbrengingsverhouding van de hoogste versnelling moet zodanig geconstrueerd worden, dat het maximale toerental van de motor behaald kan worden bij het maximale motorvermogen. Het zou zonde zijn als het toerental al tegen de begrenzing aan zit en er nog voldoende vermogensoverschot zou zijn om verder te kunnen accelereren. Behalve de hoogste versnelling moet ook de laagste versnelling zorgvuldig gekozen worden; de auto moet in de meest slechte omstandigheden probleemloos in de eerste versnelling op een helling van 40% kunnen wegrijden. Daarnaast moeten de verhoudingen van de tussenliggende versnellingen, dus 2, 3 en 4 (eventueel ook 5 als het een 6-bak betreft) daartussen bepaald worden.
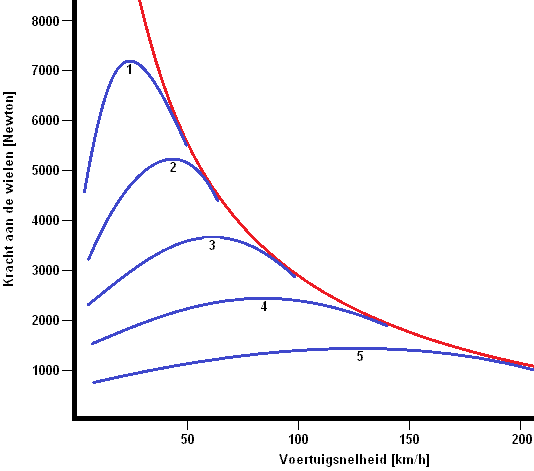
Kracht aan de wielen
In de grafiek (in de afbeelding) is de karakteristiek van de motor aangegeven met de blauwe lijnen en de voertuigkarakteristiek met de rode lijn. Hier is duidelijk te zien dat de 1e versnelling een hoge kracht aan de wielen levert (ongeveer 7200N, dus 7,2kN) en bij de hoogste versnelling (de 5e) een kracht van maximaal 1500N aan de wielen levert.
Naar mate de voertuigsnelheid en de versnellingen toenemen, daalt de geleverde kracht aan de wielen. Het verloop van de blauwe lijnen is een gevolg van de overbrengingsverhoudingen en de aflopende rode lijn is het gevolg van de rijweerstanden (de rol- en luchtweerstand).
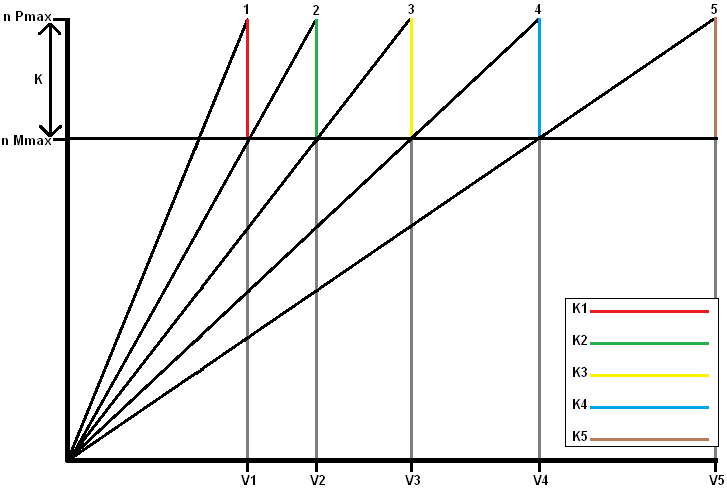
K-factor bepalen volgens de meetkundige reeks:
De volgende tekst heeft betrekking op het onderstaande zaagtanddiagram.
Als er in de eerste versnelling opgetrokken wordt tot het maximale motortoerental, moet er overgeschakeld worden naar de 2e versnelling.
Na het schakelen en ontkoppelen zal het motortoerental gedaald zijn en zal de voertuigsnelheid nog gelijk zijn. Op het moment dat er van de 1e naar de 2e versnelling geschakeld wordt, volgt het motortoerental de rode lijn in de onderstaande grafiek. Het motortoerental zal zakken van “n Pmax” naar “n Mmax”.
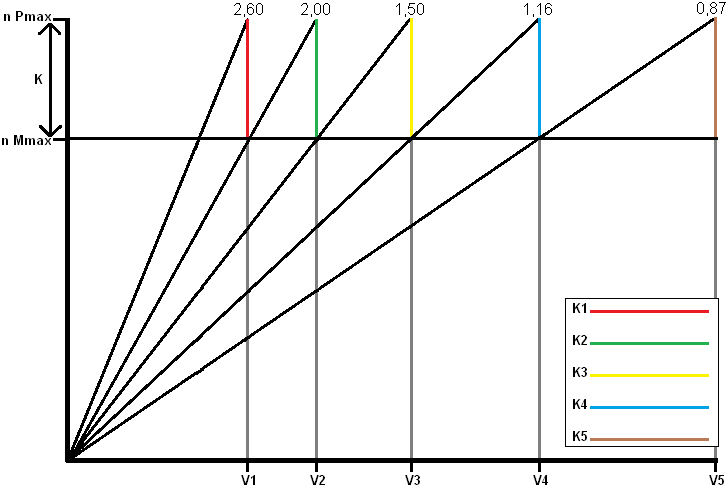
De gekleurde lijnen schetsen de K-factor. De grootte van de K-factor bepaald de grootte van de gekleurde lijnen. Liggen “n Mmax” en “n Pmax” dicht bij elkaar, dan is de K-factor klein. Er zitten dan dus kleinere gaten tussen de overbrengingen.
Met de andere versnellingen gaat het op de zelfde manier. Wordt er naar “n Pmax” van de 2e versnelling geaccelereerd (tot aan V2), wordt bij het overschakelen de groene lijn naar “n Mmax” gevolgd.
- n Pmax: Het motortoerental waarmee het maximale vermogen behaald wordt (bijv. 6000 omw./min.) met “n Pmax” als “toerental bij het maximale vermogen”
- n Mmax: Het motortoerental waarmee het maximale koppel behaald wordt (bijv. 4000 omw./min.) met “n Mmax” als “toerental bij het maximale koppel”
De verhoudingen tussen de toerentallen en de versnellingen blijven hetzelfde. Alle gekleurde lijnen (K1 t/m K5) blijven dan ook hetzelfde. De K-factor wordt bepaald door de motorkarakteristiek. De K-factor ligt tussen de motortoerentallen van het maximale koppel en het maximale vermogen van de motor. Op deze motorkarakteristiek worden dus de overbrengingen van de versnellingsbak berekend. De K-factor kan bij de meetkundige reeks als volgt bepaald worden:
K = n Pmax / n Mmax
K = 6000 / 4000
K = 1,5
Met de K-factor van 1,5 worden de reducties (overbrengingen) bepaald van alle versnellingen. Deze worden zo allemaal op elkaar afgestemd. De meetkundige reeks wordt niet toegepast op personenauto’s vanwege de te grote gaten in de hogere versnellingen. De versnellingsbakken van personenauto’s zijn ontworpen volgens de gecorrigeerde meetkundige reeks (de reeks van Jante).
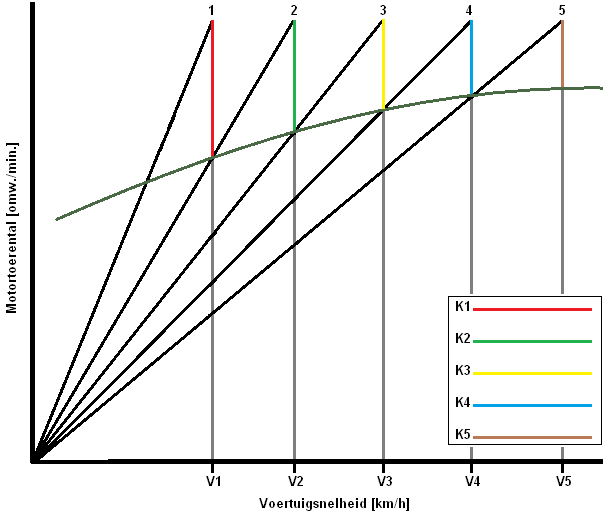
K-factor bepalen volgens de gecorrigeerde meetkundige reeks (de reeks van Jante):
Bij personenauto’s zijn de gaten tussen de lage versnellingen vaak groot en worden steeds kleiner bij de hogere versnellingen. Kleine gaten tussen de hoge versnellingen geeft weinig acceleratieverlies. De verhoudingen in de hogere versnellingen worden steeds kleiner, waardoor het motorvermogen maximaal benut wordt. Dit kun je ook merken; tussen het schakelen van de 1e naar de 2e versnelling zakt het motortoerental verder terug dan tussen het schakelen van de 3e naar de 4e versnelling. Dat is in het onderstaande zaagtanddiagram zichtbaar; de rode lijn is groter dan de gele lijn:
De rekenkundige reeks wordt ook wel “de reeks van Jante” genoemd. Het is een gecorrigeerde meetkundige reeks.
De K-factor is tussen alle versnellingen verschillend. Dit heeft grote voordelen t.o.v. de eerder genoemde meetkundige reeks met de vaste K-waarde. Doordat de verhoudingen in de hogere versnellingen steeds kleiner worden wordt het motorvermogen maximaal benut. De kracht op de wielen is nu groter dan bij de meetkundige reeks.
De K-factor is nu van elke versnelling verschillend (alle gekleurde lijnen hebben een andere lengte), dus deze moet nu allemaal met een berekening worden bepaald. Met behulp van de K-factor kunnen de overbrengingsverhoudingen van de versnellingen bepaald worden. Zonder dat de K-factor bekend is kan wel de reductie van de laagste of de hoogste versnelling bepaald worden, maar de rest van de versnellingen moeten dan berekend worden met de K-factor. Dan kan het zaagtanddiagram pas getekend worden.
Overbrengingsverhoudingen bepalen (inleiding):
De constructeur van de versnellingsbak moet met een aantal zaken rekening houden. De overbrengingen in de versnellingsbak moeten met zorg samengesteld worden. Zo zijn de factoren als de toerentallen waar de motor het meeste koppel en vermogen heeft, de dynamische bandstraal, de reductie van het differentieel en het rendement van de totale aandrijflijn van belang. Hieronder wordt dit opgesomd:
De toerentallen waar de motor het meeste koppel en vermogen heeft:
Dit zijn de toerentallen “n Pmax” en “n Mmax” die in de bovenstaande afbeelding van de meetkundige reeks staan.
De dynamische bandstraal:
Dit is de afstand tussen het hart van de naaf en het wegdek. Hoe kleiner het wiel is, des te hoger het toerental van het wiel zal zijn bij gelijke voertuigsnelheid. De dynamische bandstraal kan als volgt berekend worden (indien deze al bekend is):
De bandenmaat moet bekend zijn om dit te berekenen. Als voorbeeld nemen we de band met de maat 205/55R16. Dat betekend dat de band (205 x 0,55) = 112,75mm = 11,28cm hoog is. Omdat het 16 inch is, moet dit omgerekend worden naar centimeters: 16 x 2,54(inch) = 40,64cm.
Het gaat om de afstand tussen het wegdek en de naaf, dus de totale hoogte van 40,64cm moet nog door 2 gedeeld worden: 40,64 / 2 = 20,32 cm.
De dynamische bandstraal (Rdyn) is nu: 11,28 + 20,32 = 31,60cm.
De reductie van het differentieel:
Het differentieel heeft altijd een vaste overbrengingsverhouding. De versnellingsbak moet daar op afgestemd zijn. Bedrijfsauto’s kunnen tot wel 5 differentieels in de aandrijving hebben.
Het rendement van de totale aandrijflijn:
Door o.a. wrijvingsverliezen ontstaat er altijd een bepaald percentage verlies. Dit is ook afhankelijk van de dikte van de olie (en de temperatuur). Meestal ligt het rendement rond de 85 á 90%.
Nu gaan we de overbrengingsverhoudingen (reducties) bepalen van een fictieve motor en versnellingsbak.
De volgende specificaties zijn bekend:
- Voertuigmassa: 1500kg
- Valversnelling (G): 9,81m/s2
- Soort versnellingsbak: Handbak met 5 versnellingen en een achteruit
- Dynamische bandstraal: 0,32m (= 31,60cm uit de eerdere berekening)
- Reductie van het differentieel: 3,8:1
- Rendement aandrijflijn: 90%
- Maximale voertuigsnelheid: 220km/h (220 / 3,6 = 61,1m/s)
- Maximale helling: 20%
- Rolweerstandcoëfficiënt (μ): 0,020
- n Pmax: 100kW bij 6500 omw./min
- n Mmax: 180Nm bij 4500 omw./min

Als eerst moet bepaald worden hoeveel koppel de wielen aan het wegdek over kunnen brengen. Dit is afhankelijk van de toestand waar het voertuig zich in bevindt, want rijdt deze op een weg van asfalt met een lage rolweerstandcoëfficiënt? Samen met de rolweerstand en de dynamische bandstraal kan dit berekend worden. De formule voor de rolweerstand is als volgt:
Frol = μ x m x g x cos α (voor uitleg, zie de pagina rijweerstanden)
Frol = 0,020 x 1500 x 9,81 x cos 18 = 279,9 N
Omdat er een helling aanwezig is moet ook Fhelling worden berekend:
Fhelling = m x g x sin α
Fhelling = 1500 x 9,81 x sin 18 = 4547,2 N
De luchtweerstand kan verwaarloosd worden, dus de totale rijweerstand is als volgt:
Frij = Frol + Fhelling
Frij = 279,9 + 4547,2 = 4827,1N
Om het maximale koppel dat de wielen over kunnen brengen aan het wegdek te berekenen moet de Frij nog vermenigvuldigd worden met de dynamische bandstraal
Mwiel = Frij x Rdyn
Mwiel = 4827,1 x 0,32
Mwiel = 1544,7Nm
K-factor:
Nu gaan we de K-factor berekenen:
K = n Pmax / n Mmax
K = 6000 / 4500
K = 1,33
Reductie van de 1e versnelling berekenen:
De formule van het berekenen van de eerste versnelling is als volgt:
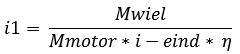
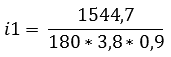
Reductie van de 5e versnelling berekenen (volgens de meetkundige reeks):
Ook de reductie van de 5e versnelling kan op een soortgelijke manier bepaald worden. De 5e versnelling moet bepaald worden aan de hand van het maximale motortoerental, want het zou vervelend zijn dat de motor nog vermogen genoeg heeft om verder te accelereren terwijl het maximale motortoerental (en dus de topsnelheid van de auto) bereikt is. Ook is het toerental van het wiel (nWiel) bij de maximale voertuigsnelheid belangrijk. Deze moet eerst berekend worden:
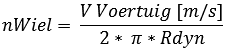
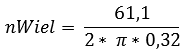
Nu het toerental van het wiel bekend is bij de maximale voertuigsnelheid van 220km/h (61,1 meter per seconde) kan de reductie van de 5e versnelling worden berekend.
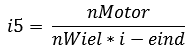
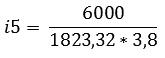
Overige reducties berekenen (volgens de meetkundige reeks):
Volgens de berekeningen is de reductie van de 5e versnelling 0,87 en de K-factor = 1,33.
Met deze gegevens kunnen (volgens de meetkundige reeks) de reducties van de 2e, 3e en de 4e versnellingen worden berekend.
i5 = (is al eerder berekend)
i4 = K x i5
i3 = K x i4
i2 = K x i3
i1 = K x i2
De reductie i1 is hier al bekend, dus als de rest correct is berekend moet er het zelfde getal (namelijk 2,51) uit komen. Een kleine afwijking is normaal, omdat er tussentijds veel afrondingen zijn gemaakt. Nu kan de rij van alle reducties ingevuld worden. Er dient van boven naar beneden gerekend te worden. Het antwoord van i5 wordt bij i4 gebruikt, en van i4 bij i3 etc.
i5 = 0,87
i4 = 1,33 x 0,87 = 1,16
i3 = 1,33 x 1,16 = 1,50
i2 = 1,33 x 1,50 = 2,00
i1 = 1,33 x 2,00 = 2,60
De tabel van de meetkundige reeks kan nu worden ingevuld.
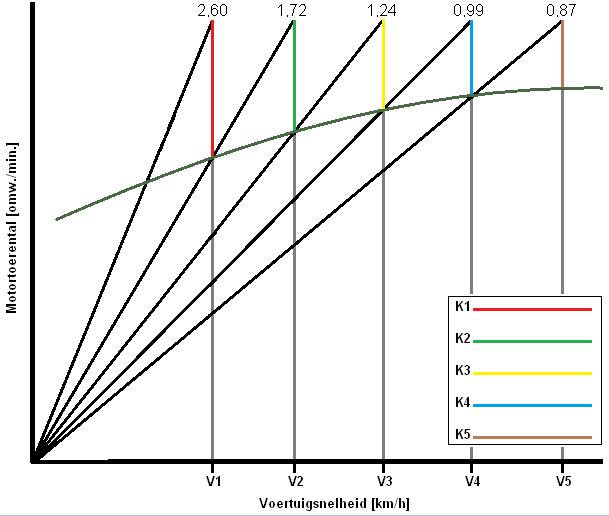
Reducties berekenen volgens de gecorrigeerde meetkundige reeks (Reeks van Jante):
Eerder op de pagina is het verschil tussen de meetkundige reeks en de “gecorrigeerde” meetkundige reeks uitgelegd. De gecorrigeerde meetkundige reeks, ook wel de “reeks van Jante” genoemd, heeft als voordeel dat de K-factor bij de hogere reducties dichter bij elkaar liggen. De K-factor bij de meetkundige reeks was constant (dit was n P max gedeeld door n M max, en bedroeg 1,33). Dit gaf in de grafiek ook een constante waarde.
Bij de gecorrigeerde meetkundige reeks loopt er in de grafiek een lijn die aangeeft dat de K-waarde niet constant is. Bij elke versnelling wordt de K-factor kleiner.
De gecorrigeerde meetkundige reeks heeft wel een constante waarde. Deze geven we aan met een m. De waarde van m = 1,1.
De algemene formule van de K-waarde van de gecorrigeerde meetkundige reeks is als volgt:
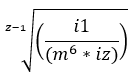
Uitleg van de formule:
z-1 = het aantal versnellingen min één
i1 = reductie eerste versnelling
m tot de zesde macht = constante tot de 6e
iz = het totaal aantal versnellingen
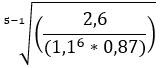
Tip: voer de vierdemachtswortel als volgt in de rekenmachine in: druk eerst de 4 in, dan SHIFT gevolgd met het wortelteken met een x-je er boven (x√). Let vervolgens op het gebruik van de haakjes voor de juiste bewerkingsvolgorde (mvdwao).
Het antwoord van de bovenstaande berekening komt uit op: 1,14
De K-waarde van de gecorrigeerde meetkundige reeks bedraagt dus 1,14. Hier gaan we verder mee rekenen:
i5 = (eerder berekend)
i4 = K x i5
i3 = K2 x m x i5
i2 = K3 x m3 x i5
i1 = K4 x m6 x i5
i5 is bekend; dit is namelijk 0,87. De K-waarde is 1,14 en m is 1,1. Met deze gegevens kunnen we het tabel invullen:
i5 = 0,87
i4 = 1,14 x 0,87
i3 = 1,142 x 1,1 x i5
i2 = 1,143 x 1,13 x i5
i1 = 1,144 x 1,16 x i5
i5 = 0,87
i4 = 0,99
i3 = 1,24
i2 = 1,72
i1 = 2,60
De tabel van de gecorrigeerde meetkundige reeks kan nu worden ingevuld:
Voertuigsnelheid per reductie berekenen (meetkundige reeks):
Per reductie kan de voertuigsnelheid bepaald worden. Dit is de snelheid dat het voertuig maximaal kan halen in deze versnelling bij het maximale toerental van 6000 omwentelingen per minuut. De berekening is als volgt:
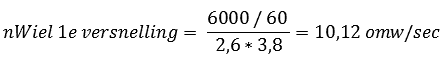
Vvoertuig 1e reductie = 2 x π x nWiel x Rdyn
(nWiel is net berekend voor de eerste versnelling en Rdyn was al bekend; deze bedraagd 0,32m. De formule kan dan ingevuld worden:
Vvoertuig 1e reductie = 2 x π x 10,12 x 0,32
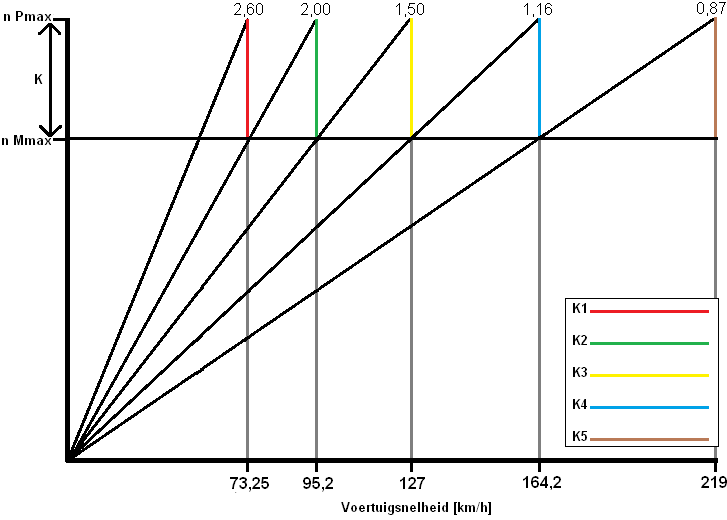
Vvoertuig 1e reductie = 20,35 m/s x 3,6 = 73,25 km/h
De andere versnellingen kunnen simpel berekend worden door de Z = 2,60 in de eerste formule te veranderen in de reductie van de gewenste versnelling, en deze vervolgens in te vullen als nWiel in de tweede formule.
De andere versnellingen hebben de volgende uitkomst:
2e versnelling: 95,2 km/h
3e versnelling: 127 km/h
4e versnelling: 164,2 km/h
5e versnelling: 219 km/h (dit is de topsnelheid van de auto)
Deze snelheden kunnen in de tabel van de meetkundige reeks worden ingevuld.
Voertuigsnelheid per reductie berekenen (gecorrigeerde meetkundige reeks):
De berekening is exact het zelfde en wordt daarom niet meer genoteerd.
1e versnelling: 73,2km/h
2e versnelling: 110,75km/h
3e versnelling: 153,61km/h
4e versnelling: 192,40km/h
5e versnelling: 219km/h
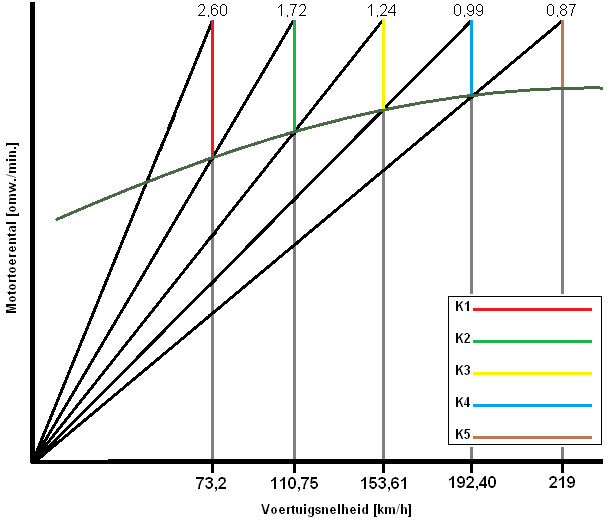
Zoals nu duidelijk is te zien zijn de topsnelheden van de auto hetzelfde bij de meetkundige- en de gecorrigeerde meetkundige reeks. Bij de meetkundige reeks (de eerste) zijn de gaten tussen de hogere versnellingen erg groot en bij de gecorrigeerde meetkundige reeks zijn de gaten tussen alle versnellingen nagenoeg gelijk. De laatst genoemde wordt bij de hedendaagse voertuigen toegepast.
