Onderwerpen:
- Condensator inleiding
- Werking van de condensator
- Serieschakeling
- Parallelschakeling
- Capacitieve niveausensor
- Op- en ontlaadtijd van de condensator (RC-tijd)
- Opladen van de condensator (met bekende laadtijd)
- Ontladen van de condensator
- Opladen van de condensator (met bekende eindspanning)
Condensator inleiding:
Condensatoren worden gebruikt in de elektrotechnische apparatuur zoals in printplaten van computers, televisies en radio’s, maar op deze pagina passen we het begrip ‘condensator’ toe op de autotechniek. In de autotechniek zijn condensatoren te vinden in o.a. elektronische filters, regelapparaten, niveaumeters, bobines en relais.
Een condensator slaat energie op. Deze energie kan bij een filter van de radio dienen als ontstoring (de condensator filtert er bepaalde frequenties uit, zoals de dynamoruis), of bij de binnenverlichting als uitschakelvertraging. Bij het sluiten van de deur gaat de binnenverlichting dan langzaam uit. Ook spanningsschommelingen van gelijkrichters (diodes) worden er mee afgevlakt. De condensator kan in korte tijd laden en ontladen.
Werking van de condensator:
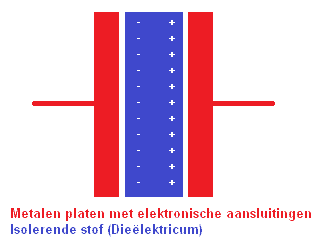
Een condensator is opgebouwd uit 2 (meestal metalen) geleiders die gescheiden zijn door het diëlektricum. Dat is een niet-geleidend materiaal zoals plastic, of anders door vacuüm.
Als er een elektronische spanningsbron op de platen wordt gezet, zullen beide platen geladen worden. De linker plaat (met de -) zal negatief geladen worden en rechter plaat (met de +) positief.
De laadstroom houdt op zodra het spanningsverschil tussen beide platen net zo groot is als het spanningsverschil op de spanningsbron. Dit laden kost tijd. Deze tijd kan berekend worden. Dit wordt later op de pagina behandeld.
De laadstroom houdt op zodra het spanningsverschil tussen beide platen net zo groot is als het spanningsverschil op de spanningsbron. Dit laden kost tijd. Deze tijd kan berekend worden. Dit wordt later op de pagina behandeld.
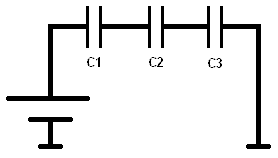
Serieschakeling met condensatoren:
Bij condensatoren die in serie geschakeld zijn, is de lading op alle condensatoren gelijk
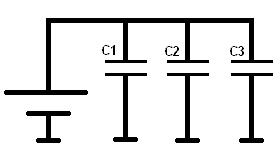
Parallelschakeling met condensatoren:
Bij parallelgeschakelde condensatoren is de spanning over alle condensatoren gelijk.
Capacitieve niveausensor:
Dit voorbeeld gaat over de niveausensor in de benzinetank van een auto. Er is sprake van een gedeeld diëlektrum.
Het principe van een capacitieve niveaumeting is gebaseerd op de verandering in de capaciteit van de condensator, dat afhankelijk is van de verandering van het niveau (in dit geval de brandstofhoeveelheid).
Benzine is geen geleidende stof, dus tussen de platen van de condensator kan geen kortsluiting ontstaan vanwege geleiding, zoals dat bij bijv. water wel het geval zal zijn.
De capaciteit van de condensator kan men bepalen met een formule. De betekenissen van de symbolen zijn als volgt:
- C = capaciteit
- A = oppervlakte plaat
- d = ruimte tussen de platen
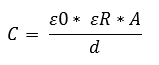
In de afbeelding is te zien dat de tank voor 40% gevuld is met benzine. De overige 60% is damp. De grijze staaf is de capacitieve condensator met afstand S (tussen de platen). Met de algemene formule kan de capaciteit, en daarmee het tankniveau worden bepaald.
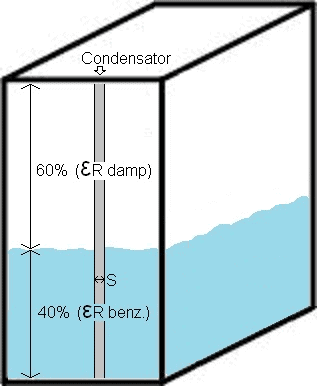
Gegevens:
Diëlektriciteitsconstanten:
ε0 (vacuüm) = 8,85 x 10-12 (macht tot de min twaalfde)
εR benzine = 2,0
εR damp = 1,18
Het oppervlakte (A) van deze condensator is 200mm² (lengte x breedte). De afstand tussen de elektroden (S) is 1,2mm
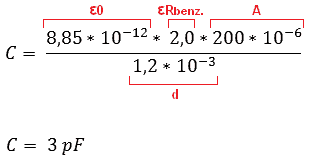
Omdat de tank 100% gevuld is, gaan we er van uit dat diëlektriciteitsconstante van benzine (2,0) over de totale oppervlakte van de condensator (200mm²) werkt. Wanneer de tank niet meer voor 100% gevuld is, maar voor 40% (zoals in de bovenstaande afbeelding), dan moet de totale oppervlakte van de condensator gedeeld worden in procenten (40% en 60% om samen 100 te maken). Daar is de 40% voor benzine, en 60% voor de damp. Er moeten daarom 2 formules worden gemaakt (C1 en C2):

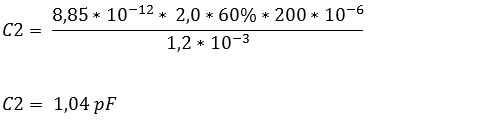
Uit de formules blijkt dat bij de 40% benzine de condensator voor 1,18 pF geladen is en bij damp 1,04 pF. Omdat de 40% en de 60% bij elkaar moeten worden opgeteld om 100% te maken, moeten de waarden van de condensator ook opgeteld worden.
Dat kan als volgt: 1,18 + 1,04 maakt 2,22 pF.
Deze 2,22 pF wordt doorgegeven aan de tankmeter op het dashboard en o.a. de ECU.
Calculator:
In plaats van zelf de formule telkens in te vullen, kunnen de gegevens ook in de calculator worden geplaatst. Deze berekent dan automatisch de capaciteit van de condensator. Ook heel handig om het berekende antwoord te controleren!
Klik op de onderstaande afbeelding om de calculator te starten. Deze opent in een nieuw scherm:

Op- en ontlaadtijd van de condensator (RC-tijd):
Als eerst wordt het begrip Tau uitgelegd:
Zodra een condensator met een weerstand in serie wordt geplaatst, zal de condensator opgeladen worden tot de aangelegde spanning (de bronspanning oftewel de accuspanning) bereikt wordt. Vastgesteld is, dat de condensator is geladen tot 63,2% van de aangelegde spanning na 1 (Tau). Bij 5 is de condensator voor 99,3% geladen. (Theoretisch gezien zal de condensator nooit volledig 100% geladen worden). Aan de hand van de volgende afbeelding wordt dit duidelijk gemaakt:
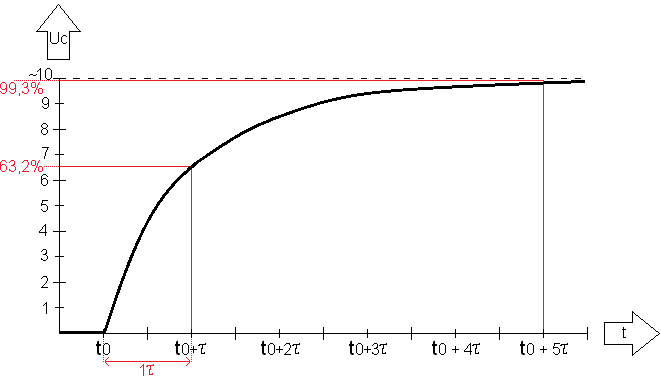
In de bovenstaande grafiek is het opladen van de condensator te zien. Bij t0 schakelt de condensator in, en is bij t0 + 5 geladen.
Bij het tijdstip t0+ (op de x-as) is de condensator precies 1 geladen, omdat deze bij tijdstip t0 ingeschakeld werd. Op de Y-as is te zien dat dit op 63,2% is van Uc. Bij het tijdstip t0+5 is de condensator 99,3% geladen.
Met de formule = R x C wordt de hoeveelheid (Tau) berekend.
In de onderstaande schakeling staan 2 weerstanden in serie met elkaar. De totale weerstand is dus R1+R2. Dit maakt dus 10+10=20k. (20×10^3). Vermenigvuldigd met C van 10 Microfarad (10×10^-6) maakt dat (200×10^-3) = 0,2.
Deze 0,2 moet dalijk in de berekening ingevuld worden.
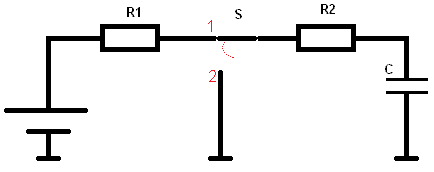
R1 = 10k
R2 = 10k
C = 10µ
Zowel de weerstandwaarden als de capaciteit van de condensator bepalen de op- en ontlaadtijd van de condensator. De snelheid waarmee de condensator moet laden en ontladen kan erg belangrijk zijn. Zeker in schakelingen in microprocessoren zal deze tijd zeer kort moeten zijn. Bij de uitschakelvertraging van de binnenverlichting van de auto zal de tijd wel groot mogen zijn. De algemene formule van de schakeltijden is als volgt:
Uct staat voor de spanning in een bepaalde tijd. Deze tijd wordt berekend in de formule. Uct 0 is de beginspanning, waar het opladen of ontladen begint. Uct ~ (teken voor oneindig) staat voor de spanning welke het maximaal kan worden (dat is de aangelegde spanning / accuspanning). De e staat voor de e-macht. Dit is een natuurlijk logaritme. Het is een exponentieel getal. De -(t1 – t0) gedeeld door τ (Tau) staat nu in machtsvorm. Het moet dus ook uitgesproken en berekend worden als e tot de macht -(t1 – t0) gedeeld door τ.
Daarna volgt + Uct ~. Dit is ook weer de aangelegde spanning / accuspanning.
Als deze berekening is uitgevoerd, komt daar een antwoord uit in volt (spanning).
In de volgende paragraaf volgt een voorbeeld met een schakeling:
Laden van de condensator (met bekende laadtijd):
In de afbeelding staat de schakelaar gesloten. Er loopt een stroom van de accu via de weerstanden naar de condensator. We willen de spanning berekenen wanneer de condensator 200 milliseconden lang geladen is (200 x 10^-3).

U = 10 v
R1 = 10k
R2 = 10k
C = 10 µF (Microfarad).
τ = R x C
τ = (10.000 + 10.000) x 0,000010 = 0,2
τ = 200 x 10^-3
In formulevorm wordt dit:
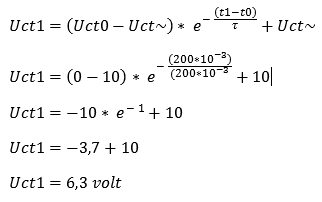
Vanaf t0 naar t1 is de condensator met 6,3 volt geladen. Dit is gelijk aan 1τ (want bij 1 is de condensator voor 63,2% geladen). De grafiek ziet er n.a.v. de berekening dan als volgt uit:
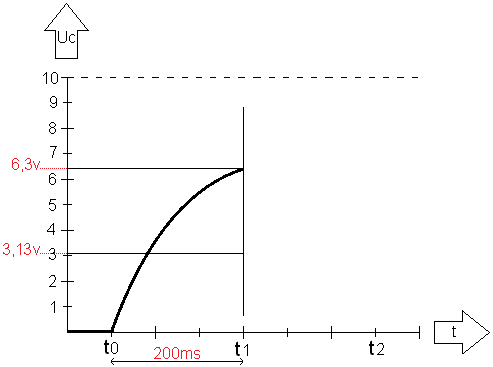
Ontladen van de condensator:
Nu gaan we de condensator ontladen. De schakelaar in het schema wordt van stand 1 naar stand 2 verplaatst. De spanningsbron (de accu) wordt uit het circuit van de condensator verbroken. In het schema zijn beide zijden van de condensator verbonden met de massa (via weerstand R2). De condensator gaat nu ontladen. Ook nu geldt dat de weerstandwaarde en de capaciteit van de condensator de ontlaadtijd bepalen, net als dat bij het opladen het geval was. Echter, er is nu een weerstand minder (want R1 staat niet meer in het zelfde circuit). Daarom zal de ontlaadtijd nu korter zijn dan de laadtijd:
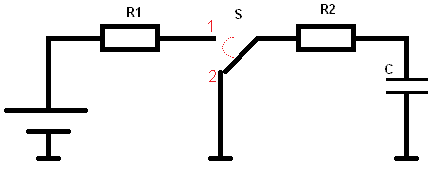
Nu vullen we de formule weer in om de Tau te berekenen:
τ = R x C
τ = 100.000 x 0,001
τ = 100
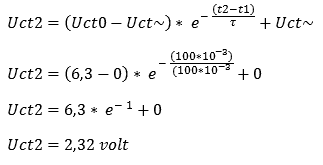
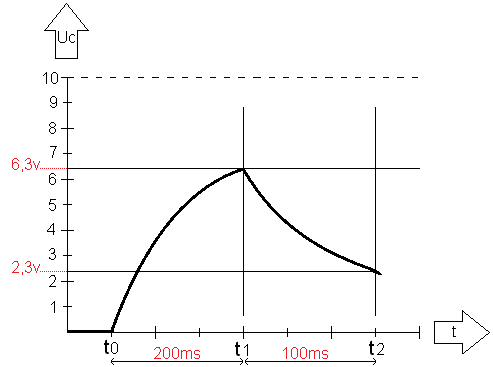
Volgens de formule is de condensator na 100ms ontladen tot 2,32 volt. Wanneer we t1-t2 niet zouden meten over 100ms maar over 200ms, dan zou de grafiek weer bijna op 0 volt uit komen. Het laden kost wel meer tijd dan het ontladen, omdat bij het ontladen er 1 weerstand in het circuit zit, i.p.v. bij het laden, waarbijf er 2 weerstanden in serie geschakeld zijn. De condensator zal dus in principe meer tijd nodig hebben dan 200ms om op 0 volt te komen. Als de schakelaar bij t2 weer omgezet worden naar stand 1, dan zou de condensator weer direct beginnen met laden.
De periode van ontladen kunnen we vervolgens in de grafiek zetten:
Laden van de condensator (met bekende eindspanning):
Bij het laden van de condensator het in bovenstaande voorbeeld was de laadtijd (van 200ms) bekend. Met de gegevens van begin- eindspanning, de laadtijd en het aantal Tau kon de eindspanning worden berekend. De condensator was dan na 200ms met 6,3 volt geladen.
Nu komen we in de situatie waarbij de laadtijd onbekend is, maar de eindspanning wel al gegeven is. Voor het gemak gebruiken we hetzelfde voorbeeld;
(De weerstandwaardes en het type condensator zijn hetzelfde als in het eerste voorbeeld).

R1 = 10k
R2 = 10k
C = 10µF (Microfarad).
τ = R x C
τ = (10.000 + 10.000) x 0,000010 = 0,2
τ = 200 x 10^-3
Wat we nu willen weten is, hoeveel tijd kost het (van t0 naar t1) om de condensator tot 6,3 volt te laden?
Door de bekende gegevens in de formule van de 1e orde differentiaalvergelijking in te vullen, lukt het niet direct om er een antwoord uit te verkrijgen. De formule moet namelijk omgevormd worden, omdat -(t1 – t0) onbekend is en we die in principe willen weten.
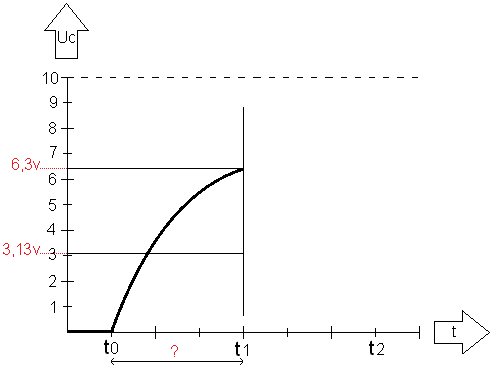
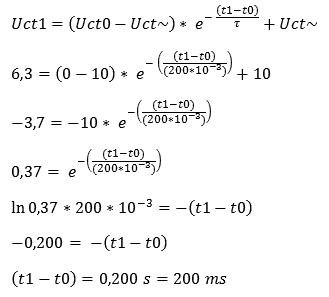
Uitleg: Als eerst wordt de basisformule opgesteld. Deze vullen we in met de gegevens die bekend zijn. Omdat we de tijd willen weten bij een laadtijd van 6,3 volt, vullen we deze in het begin van de formule in. De (t1 – t0) blijft zo genoteerd staan.
Vervolgens delen we de Uct~ van 10 v door de 6,3 v links in de formule, waar het antwoord van 3,7 v uit komt. De +10 kan nu worden weggestreept.
De volgende stap is om de -10 (getal voor de e-macht) te elimineren. Door de -3,7 door -10 te delen, vervalt deze. Links in de formule vullen we nu 0,37 in.
Nu is het tijd om de e-macht de elimineren. De inverse van een e-macht is de ln, een natuurlijke logaritme, (net zoals van een macht de inverse de wortel is).
Door in de rekenmachine de formule met de ln-knop in te toetsen, komt daar als antwoord -0,200 uit. Door dat links en rechts van het = teken negatief is, kunnen de mintekens worden weggestreept.
Als antwoord komt hier 200 ms uit. Dus de condensator doet er 200 ms over om tot 6,3 volt geladen te worden. Dat klopt, want in de eerste berekening van de oplaadtijd was dit een gegeven, waarmee de 6,3 volt berekend moest worden.
Met deze formule kan ook de tijd bij bijv. 3 volt berekend worden. Verander dan de 6,3 volt in 3 volt, haal daar 10 volt vanaf, deel deze door -10 volt, vermenigvuldig deze weer met de ln en de 200 . 10^-3. Er komt dan een antwoord uit van 71 ms.
