Onderwerpen:
- Inleiding
- Brug van Wheatstone in balans
- Ongebalanceerde brug van Wheatstone (weerstandswaarden bekend)
- Brug van Wheatstone met onbekende weerstandswaarde
Inleiding:
De brug van Wheatstone is een elektrische brugschakeling voor het nauwkeurig meten van een gelijkblijvende of veranderende elektrische weerstand. Deze schakeling kan worden gebruikt om fysische grootheden zoals temperatuur en druk te meten, zoals we zien in de luchtmassameter (temperatuur van de hittedraad) en MAP-sensor (druk in het inlaatspruitstuk).
In de brug van Wheatstone bevinden zich vier weerstanden, waarvan drie met een bekende, en één met een onbekende weerstand. Daarmee bestaat de brug in feite uit twee spanningsdelers die parallel aan elkaar staan geschakeld.
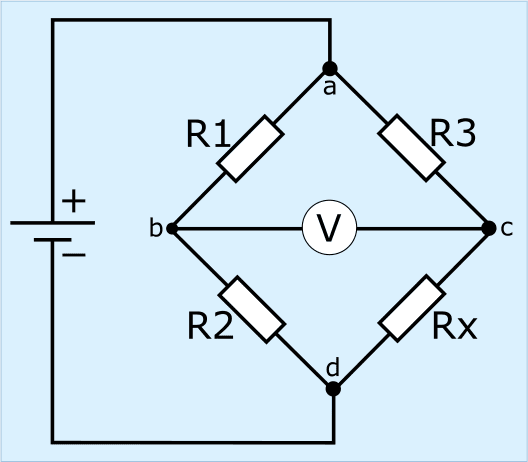
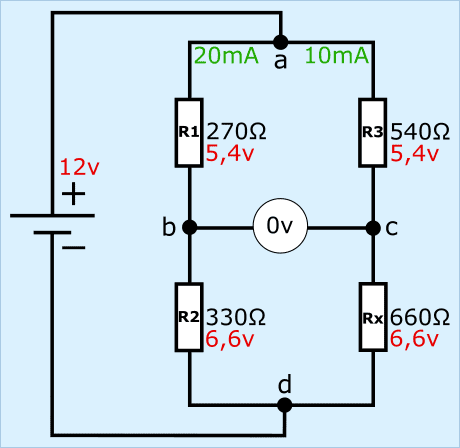
In de afbeelding zien we de weerstanden R1 t/m R3 (bekende weerstandwaardes) en Rx (onbekend), met in het midden van de twee spanningsdelers een voltmeter en links van de brug een spanningsbron.
De brug van Wheatstone is in evenwicht of gebalanceerd als de uitgangsspanning tussen de punten b en c gelijk is aan 0 volt. In de volgende paragrafen worden verschillende situaties getoond.
Brug van Wheatstone in balans:
De Wheatstonebrug is gebalanceerd of in evenwicht als de uitgangsspanning gelijk is aan 0 volt, doordat de weerstandswaardes links en rechts met elkaar in verhouding zijn.
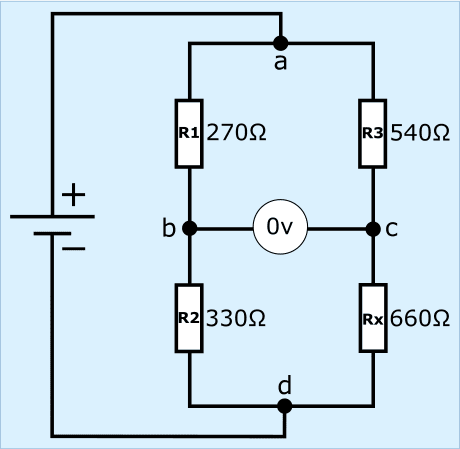
De schakeling in deze paragraaf is anders getekend dan in de vorige paragraaf, maar berust op dezelfde werking.
- de weerstanden R1 en R2 hebben een weerstand van 270 en 330 Ω. Bij elkaar opgeteld is dit 600 Ω;
- de weerstanden R3 en Rx hebben een weerstand van 540 en 660 Ω. Bij elkaar opgeteld is dit 1200 Ω.
De verhoudingen tussen de weerstanden links en rechts is gelijk aan elkaar. Daarmee zijn de weerstandsverhoudingen en de spanningsvallen gelijk aan elkaar tussen R1 en R3, alsmede R2 en Rx.
In de onderstaande formules worden de gelijke weerstandsverhoudingen en de spanningsvallen getoond:
![]() en
en ![]()
Bij een bekende voedingsspanning en weerstandswaardes, kunnen we de spanningsvallen over de weerstanden, en daarmee het spanningsverschil tussen de punten b en c bepalen. In het onderstaande voorbeeld berekenen we het spanningsverschil tussen punten b en c bij een gebalanceerde Wheatstonebrug. De kennis van de Wet van Ohm en rekenen met serie- & parallelschakelingen is een vereiste.
1. berekenen van de stromen door weerstanden R1 en R2 (RV = vervangingsweerstand):
![]()
2. bereken de spanningsval over de weerstanden R1 en R2:
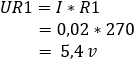
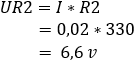
3. bereken de stromen door de weerstanden R1 en R2:![]()
4. bereken de spanningsval over de weerstanden R3 en Rx:
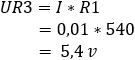
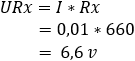
De spanning op punt b en c bedraagt 5,4 volt. Het potentiaalverschil is gelijk aan 0 volt.
Ongebalanceerde brug van Wheatstone (weerstandswaarden bekend):
Ten gevolge van een weerstandsverandering van Rx zal de Wheatstonebrug uit balans raken. De weerstandsverandering kan optreden door bijvoorbeeld een veranderende temperatuur, waarbij Rx een thermistor is. De spanningsdeler tussen R1 en R2 zal gelijk blijven, maar tussen R3 en Rx niet. Doordat daar de spanningsdeler verandert, krijgen we op punt c een andere spanning. In dit voorbeeld is de weerstandswaarde van Rx van 600 Ω naar 460 Ω gedaald.
1. berekenen van de stromen door weerstanden R1 en R2:
![]()
2. bereken de spanningsval over de weerstanden R1 en R2:
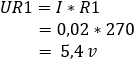
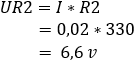
4. bereken de spanningsval over de weerstanden R3 en Rx:
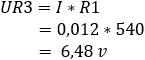
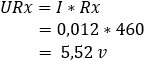
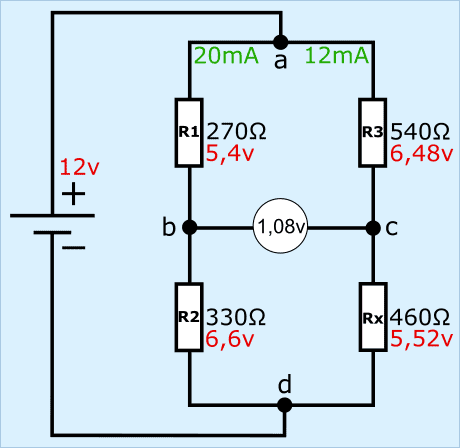
In de twee voorbeelden is de weerstandswaarde van Rx veranderd van 660 Ω naar 460 Ω. Door deze weerstandsverandering is de spanning tussen b-c van 0 volt naar 1,08 volt veranderd. Als deze brug van Wheatstone in de sensorelektronica is ingebouwd, wordt de spanning van 1,08 volt als signaalspanning gezien. Deze signaalspanning wordt via een signaaldraad naar de ECU gestuurd. De A/D-converter in de ECU zet de analoge spanning om in een digitaal bericht, welke door de microprocessor kan worden gelezen.
Brug van Wheatstone met onbekende weerstandswaarde:
In de vorige paragrafen gingen we uit van een bekende weerstandswaarde van Rx. Omdat deze weerstandswaarde variabel is, kunnen we een stapje verder gaan door deze weerstandswaarde te gaan berekenen om de brug van Wheatstone in balans te brengen.
In deze schakeling bedragen R1 en R2 wederom 270 en 330 Ω. De weerstand van R3 is verlaagd naar 100 Ω en Rx is onbekend. Als naast de weerstandswaarde ook de spanningen en stromen onbekend zijn, kunnen we op twee manieren de weerstandswaarde Rx berekenen:
Manier 1:
1. we bekijken eerst de algemene formule en vullen vervolgens de weerstandswaardes in:
![]() –>
–> ![]()
2. tussen 270 en 100 zit een factor 2,7, evenals tussen 330 en de onbekende waarde.
Door 330 te delen door 2,7 komen we op een weerstand van 122,2 Ω uit.
![]()
Manier 2:
1. via de algemene formule waarin we de weerstanden kruislings vermenigvuldigen:
![]()
2. we bouwen de formule om door Rx aan de linkerkant van = te halen en te delen door R1. Hierbij komen we eveneens op de weerstandswaarde uit van 122,2 Ω.
![]()
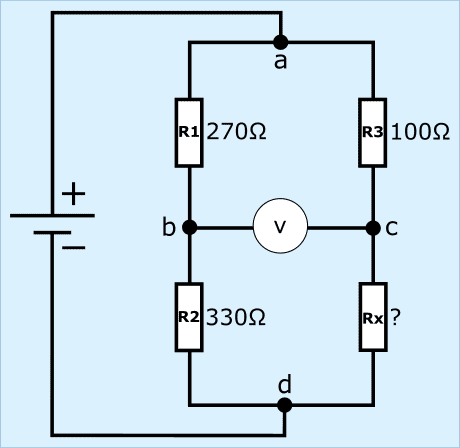
Uiteraard checken we of we een gebalanceerde brug hebben met de eerder berekende weerstand van 122 Ω.
De weerstanden R1 en R2 met de stromen en deelspanningen zijn hetzelfde als in de voorbeelden in paragraaf 1 en 2, dus die worden als bekend beschouwd. We richten ons op de rechterzijde van de brug.
1. bereken de stroom door R3 en Rx:
![]()
2. bereken de spanningsval over de weerstanden R3 en Rx:
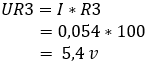
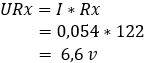
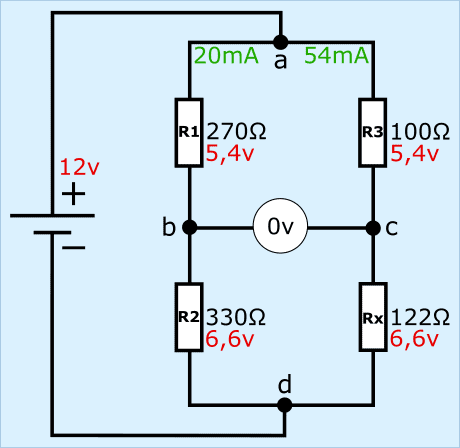
Het spanningsverschil tussen de punten b en c bedraagt 0 volt omdat de weerstanden R1 en R3 beiden 5,4 opnemen, dus de brug is nu in balans.
Gerelateerde pagina’s:
