Onderwerpen:
- Aslast berekenen door middel van VLS
- Aslast voorzijde berekenen
- Verschil tussen gewicht en massa
- Aslast achterzijde berekenen
- Kogeldruk berekenen
- Invloed van de kogeldruk op de achteras berekenen
Aslast berekenen door middel van VLS:
De aslasten van een voertuig kunnen berekend worden met een schematische tekening en de gegevens van de auto. Door middel van een VLS (Vrij Lichaam Schema) kan een auto met de desbetreffende krachten getekend worden (zie onderstaande afbeelding). De voorwaarden van een VLS zijn, dat het wegdek niet getekend wordt. Ook als het voertuig op een heuvel staat mag het voertuig niet schuin getekend worden, maar moet er een horizontale kracht met een richting in het VLS getekend worden.
Het voordeel met het werken met een VLS is dat de onnodige dingen worden weggelaten. Wanneer bijv. de inwendige momenten of aslast van een aanhanger te berekenen, is het handig om alleen de aanhanger te tekenen i.p.v. een auto met aanhanger. Door alleen te tekenen wat nodig is, voorkom je het maken van fouten (door te veel horizontale / verticale krachten mee te nemen in de berekening die er niet in thuis horen).
Als eerste dient het gewicht d.m.v. de zwaartekrachtversnelling berekend te worden die op het voertuig werkt. De zwaartekracht is afhankelijk van de plek op de aarde waarin het voertuig zich bevindt. In Nederland bedraagt de zwaartekrachtversnelling 9,81m/s.
De voertuigmassa moet met de zwaartekracht vermenigvuldigd worden. Dat geeft: 1500 x 9.81 = 14.715N (De eenheid van kracht is Newton). Hier moet nog wel even bij vermeld worden dat de zwaartekrachtversnelling soms ook gravitatieversnelling, gravitatieconstante of valsnelheid wordt genoemd. Ook wordt het getal 9,81 soms afgerond als 9,8 of heel ruw als 10. Dit is wel makkelijker rekenen (1500 / 10 is makkelijker uit het hoofd te berekenen dan 1500/ 9.81) maar het eindantwoord is zeker niet nauwkeurig. Pas daarom altijd de 9,81m/s toe, tenzij het in een bijv. een tentamenvraag anders wordt gesteld.
De totale kracht waarmee het voertuig op het wegdek wordt gedrukt is dus 14.715 Newton. Deze kracht is verdeeld over beide assen van de auto.
Vaak is de aslast aan de voorzijde hoger, omdat daar de motor zit. Dat is in de afbeelding te zien aan het zwaartepunt, dat vanuit het midden gezien aan de voorkant zit. Het zwaartepunt is een denkbeeldig draaipunt. Zou dit zwaartepunt exact in het midden zitten, is de aslast op beide assen gelijk (voertuigmassa delen door 2). Doordat de afstanden van de wielen, de plaats van het zwaartepunt en de totale voertuigmassa bekend zijn, kunnen de aslasten aan de voor- en achterzijde worden berekend.
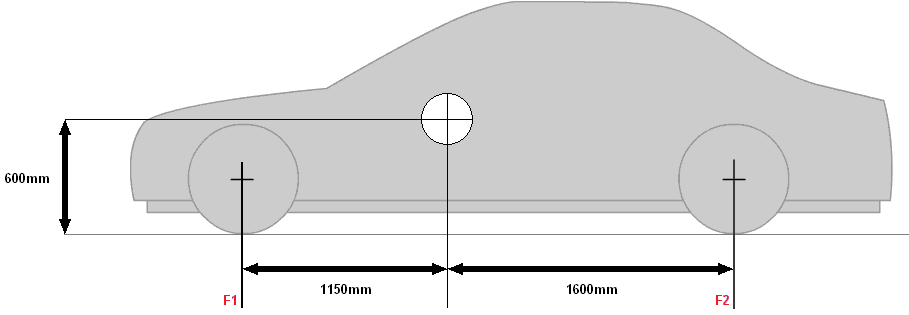
Voertuigmassa: 1500kg
Gewicht: 14715N
Hoogte wegdek – knikpunt: 60cm
Afstand F1 – knikpunt: 115cm
Afstand knikpunt – F2: 160cm
Afstand F1 – F2: 115+160= 275cm (dit is de wielbasis)
Aslast F2 (achteras) berekenen:
14715 x 1,15 – F2 x 2,75 = 0
16922 – F2 x 2,75 = 0
F2 = 16922 / 2,75
F2 = 6154N
De berekening staat hieronder uitgebreid uitgewerkt:
- Om F1 en F2 te berekenen, moet er eerst één berekend worden. We kiezen er voor om F2 als eerst te berekenen.
We maken bij F1 het draaipunt. Alles rechtsom is positief en alles linksom is negatief. Dat betekent dat de krachten die omlaag zijn gericht positief zijn, en de kracht F2 omhoog is negatief. We vullen het eerste gedeelte van de formule in.
14715 x 1,15 – F2 x 2,75 = 0
(Deze laatste 0 standaard invullen, want verder in de berekening worden de getallen links- en rechts van het ” = ” teken gewisseld) - Kracht x arm: Het gewicht van 14715 wordt met de afstand van 1,15 vermenigvuldigd:
14715 x 1,15 = 16922 - Nu vullen we deze weer in de formule in:
16922 – F2 x 2,75 = 0 - Verplaats de 16922 naar de andere kant waar de 0 staat:
F2 x 2,75 = 16922 - Deel beide kanten door 2,75 om deze links van het = teken te verwijderen:
F2 = 16922 / 2,75 - Dat resulteert in:
F2 = 6154N.
Verschil tussen gewicht en massa:
Onthoud dat het gewicht niet hetzelfde als massa is. Het gewicht van F2 is in de vorige berekening 6154 Newton. Een massa is altijd in kilogram. Het moet daarom altijd door de zwaartekrachtversnelling van 9,81 gedeeld worden. (6154 / 9,81 = 627,3kg) Denk maar aan het massa ledig voertuig dat op het kentekenbewijs vermeld staat. Dat staat ook altijd in kg. Om het bovenstaande verhaal duidelijk te maken; In de ruimte is geen zwaartekracht aanwezig. Alles zweeft daar, ongeacht hoe zwaar het is. Alles heeft wel degelijk een gewicht; wanneer je een pak melk ergens tegen aan gooit, of een steen, dit zal een andere impact hebben. Het pak melk zal niet snel iets beschadigen wanneer het bijv. de muur raakt, maar de steen zal wel degelijk schade aanbrengen. Dat komt door dat de kracht waarmee het voorwerp tot stilstand komt, bij de steen hoger is dan bij het pak melk. Dit bewijst dat het gewicht óók in de ruimte aanwezig is en van belang is, maar de massa niet. De massa komt door de aantrekkingskracht van de aarde. Dus het gewicht van de auto is niet 1200kg, maar de massa is 1200kg. Hier worden vaak veel fouten mee gemaakt.
Aslast aan de achterzijde berekenen:
Wanneer het totale gewicht en 1 aslast bekend zijn, kan heel gemakkelijk de 2e aslast worden berekend door deze twee van elkaar af te trekken:
Totaal gewicht – F2 = F1:
14715 – 6154 = 8561N.
F1 kan natuurlijk ook apart berekend worden. Dat gaat bijna het zelfde als de eerste berekening:

14715 x 1,6 – F1 x 2,75 = 0
23544 – F1 x 2,75 = 0
F1 = 23544 / 2,75
F1 = 8561N
De kracht dat het voorwiel op het wegdek uitoefent is 8561N en het achterwiel 6154N. Bij elkaar opgeteld is dit 14715N. De totale voertuigmassa is dus 14715 / 9.81 = 1500kg.
Kogeldruk berekenen:
Met dezelfde manier als dat de aslasten bij de auto in de vorige hoofdstukken berekend werden, kan ook de kogeldruk op de trekhaak van de auto bepaald worden. Moment is kracht x arm. Dat wil dus zeggen, hoe langer de arm is, hoe groter het moment wordt. De aslast achter is afhankelijk van de afstand tussen F2 en F3 en de kogeldruk is afhankelijk van de afstand tussen F3 en F4. En juist de kracht op ‘het scharnierpunt’, of te wel de trekhaakkogel moet berekend worden.
De auto is 1500kg, en de aanhanger 300kg. Deze rekenen we eerst weer om naar Newton door te vermenigvuldigen met de zwaartekrachtversnelling:
1500 x 9,81 = 14715N
300 x 9,81 = 2943N
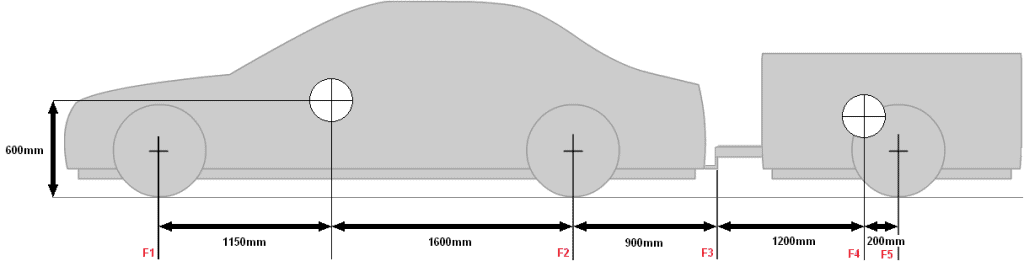
Om de kogeldruk te berekenen is het makkelijker om eerst alleen de aanhanger te tekenen. De auto zelf is in de berekening niet belangrijk.
De kogeldruk wordt aangegeven met F3 en de kracht waarmee de band op het wegdek drukt F5.
F3 wordt het draaipunt en we gaan de kracht F5 berekenen. Het zwaartepunt is een kracht naar onderen, dus positief. De kracht die op F5 werkt, is een kracht omhoog, dus deze is negatief (dus er komt een minteken voor te staan). Het gewicht van de aanhanger is 4000N.
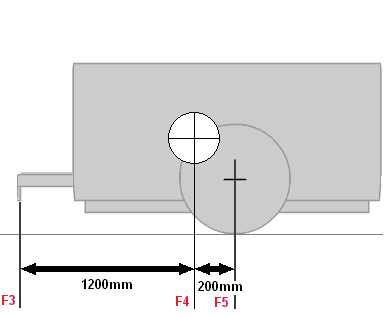
De kracht F5 berekenen:
4000 x 1,2 – F5 x 1,4 = 0
4800 – F5 x 1,4 = 0
F5 = 4800 / 1,4
F5 = 3429N
De kogeldruk (F3) berekenen:
4000 – 3429 = 571N
571 / 9,81 = 58,2kg
De kogeldruk met deze aanhanger is 58,2kg.
Als het zwaartepunt naar achteren beweegt, wordt de kogeldruk kleiner. Om dit inzicht te krijgen en te oefenen met de berekeningen, is het handig om de afstand tussen F3 en F4 en dus ook tussen F4 en F5 groter en kleiner te maken en de berekening opnieuw uit te voeren.
Invloed van de kogeldruk op de achteras berekenen:
Doordat de kogeldruk nu bekend is, kan berekend worden wat voor invloed dit heeft op de achteras. Het gewicht kan niet zomaar erbij opgeteld worden, omdat de afstand tussen de achteras en de trekhaakkogel van groot belang is (kracht x arm). We pakken weer dezelfde afbeelding van de auto met aanhanger.

In de vorige berekening was bekend geworden dat de kogeldruk (F3) 571N bedraagt. F2 was ook al bekend, dat was namelijk 6154N. De krachten kunnen niet bij elkaar worden opgeteld, omdat de afstand tussen het achterwiel en de kop van de trekhaakkogel nog als arm functioneert. We maken de gehele formule opnieuw, zoals helemaal aan het begin van deze pagina. Bij deze formule komt dan 571 x 3,65 er nog bij (de kracht op F3 met de afstand vanaf F1 tot F3 daarbij opgeteld).
14715 x 1,15 + 571 x 3,65 – F2 x 2,75 = 0
19006 – F2 x 2,75 = 0
F2 = 19006 / 2,75
F2 = 6911N = 691kg.
Dat betekent dat op de achteras een gewicht van 691kg staat.
